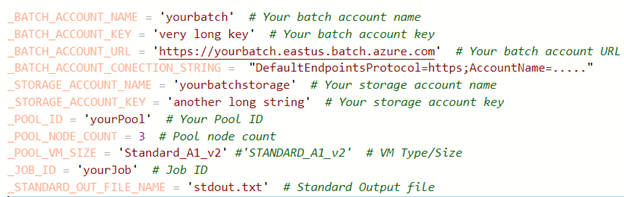
Introduction
As an organization or enterprise grows, the knowledge needed to keep it going explodes. The shear complexity of the information sustaining a large operation can become overwhelming. Consider, for example the American Museum of Natural History. Who does one contact to gain an understanding of the way the different collections interoperate? Relational databases provide one way to organize information about an organization, but extracting information from an RDBMS can require expertise concerning the database schema and the query languages. Large language models like GPT4 promise to make it easier to solve problems by asking open-ended, natural language questions and having the answers returned in well-organized and thoughtful paragraphs. The challenge in using a LLM lies in training the model to fully understand where fact and fantasy leave off.
Another approach to organizing facts about a topic of study or a complex organization is to build a graph where the nodes are the entities and the edges in the graph are the relationships between them. Next you train or condition a large language model to act as the clever frontend which knows how to navigate the graph to generate accurate answers. This is an obvious idea and others have written about it. Peter Lawrence discusses the relation to query languages like SPAQL and RDF. Venkat Pothamsetty has explored how threat knowledge can be used as the graph. A more academic study from Pan, et.al. entitled ‘Unifying Large Language Models and Knowledge Graphs: A Roadmap’ has an excellent bibliography and covers the subject well.
There is also obvious commercial potential here as well. Neo4J.com, the graph database company, already has a product linking generative AI to their graph system. “Business information tech firm Yext has introduced an upcoming new generative AI chatbot building platform combining large language models from OpenAI and other developers.” See article from voicebot.ai. Cambridge Semantics has integrated the Anzo semantic knowledge graph with generative AI (GPT-4) to build a system called Knowledge Guru that “doesn’t hallucinate”.
Our goal in this post is to provide a simple illustration of how one can augment a generative large language model with a knowledge graph. We will use AutoGen together with GPT4 and a simple knowledge graph to build an application that answers non-trivial English language queries about the graph content. The resulting systems is small enough to run on a laptop.
The Heterogeneous ACM Knowledge Graph
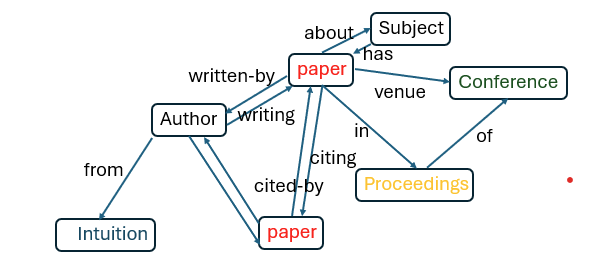
To illustrate how to connect a knowledge graph to the backend of a large language model, we will program Microsoft’s AutoGen multiagent system to recognize the nodes and links of a small heterogeneous graph. The language model we will use is OpenAI’s GPT4 and the graph is the ACM paper citation graph that was first recreated for a KDD cup 2003 competition for the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Its current form, the graph consists of 17,431 author nodes from 1,804 intuition nodes, 12,499 paper titles and abstracts nodes from 14 conference nodes and 196 conference proceedings covering 73 ACM subject topics. It is a snapshot in time from the part of computer science represented by KDD, SIGMOD, WWW, SIGIR, CIKM, SODA, STOC, SOSP, SPAA, SIGCOMM, MobilCOM, ICML, COLT and VLDB. The edges of the graph represent (node, relationship, node) triples as follows.
- (‘paper’, ‘written-by’, ‘author’)
- (‘author’, ‘writing’, ‘paper’)
- (‘paper’, ‘citing’, ‘paper’)
- (‘paper’, ‘cited-by’, ‘paper’)
- (‘paper’, ‘is-about’, ‘subject’)
- (‘subject’, ‘has’, ‘paper’)
- (‘paper’, ‘venue’, ‘conference’)
- (‘paper’, ‘in’, ‘;proceedings’)
- (‘proceedings’, ‘of-conference’, ‘conference’)
- (‘author’, ‘from’, ‘institution’)
Figure 1 illustrates the relations between the classes of nodes. (This diagram is also known as the metagrapah for the heterogeneous graph.) Within each class the induvial nodes are identified by an integer identifier. Each edge can be thought of as a partial function from one class of nodes to another. (It is only a partial function because a paper can have multiple authors and some papers are not cited by any other. )

Figure 1. Relations between node classes. We have not represented every possible edge. For example, proceedings are “of” conferences, but many conferences have a proceeding for each year they are held.
Connecting the Graph to GPT4 with AutoGen.
Autogen is a system that we have described in a previous post, so we will not describe it in detail here. However the application here is easy to understand. We will use a system of two agents.
- A UserProxyAgent called user_proxy that is capable of executing the functions that can interrogate our ACM knowledge graph. ( It can also execute Python program, but that feature is not used here.)
- An AssistantAgent called the graph interrogator. This agent takes the English language search requests from the human user and breaks them down into operations that can be invoked by the user_proxy on the graph. The user_proxy executes the requests and returns the result to the graph interrogator agent who uses that result to formulate the next request. This dialog continues until the question is answered and the graph interrogator returns a summary answer to the user_proxy for display to the human.
The list of graph interrogation functions mirrors the triples that define the edges of the graph. They are:
- find_author_by_name( string )
- find_papers_by_authors (id list)
- find_authors (id list)
- paper_appeared_in (id list)
- find_papers_cited_by (id list)
- find_papers_citing (id list)
- find_papers_by_id (id list)
- find_papers_by_title (string )
- paper_is_about (id list)
- find_papers_with_topic (id list)
- find_proceedings_for_papers (id list)
- find_conference_of_proceedings (id list)
- where_is_author_from (id list)
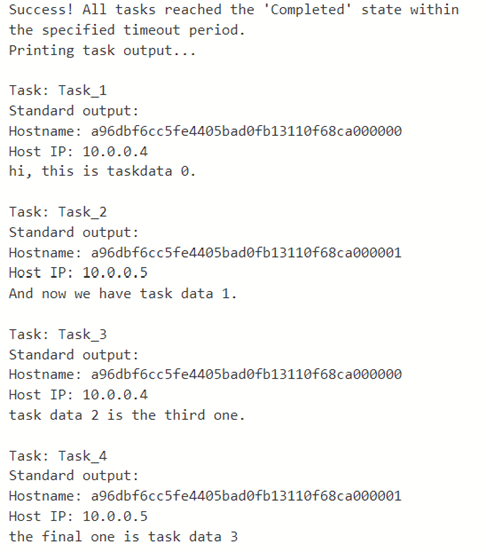
Except for find_author_by_name and find_papers_by_title which take strings for input, the others all take graph node id lists. They all return nod id lists or list of (node id, strings) pairs. It is easiest to understand the dialog is to see an example. Consider the query message.
Msg = ‘Find the authors and their home institutions of the paper “A model for hierarchical memory”.’
We start the dialog by asking the user_proxy to pass this to the graph_interrogator.
user_proxy.initiate_chat(graph_interogator, message=msg)
The graph interrogator agent responds to the user proxy with a suggestion for a function to call.

Finally, the graph interrogator responds with the summary:

To compare this to GPT-4 based Microsoft Copilot in “precise” answer mode, we get:

Asking the same question in “creative” mode, Copilot lists four papers, one of which is correct and has the authors’ affiliation as IBM which was correct at the time of the writing. The other papers are not related.
(Below we look at a few more example queries and the responses. We will skip the dialogs. The best way to see the details is to try this out for yourself. The entire graph can be loaded on a laptop and the AutoGen program runs there as well. You will only need an OpenAI account to run it, but it may be possible to use other LLMs. We have not tried that. The Jupyter notebook with the code and the data are in the GitHub repo.)
Here is another example:
msg = ”’find the name of authors who have written papers that cite paper “Relational learning via latent social dimensions”. list the conferences proceedings where these papers appeared and the year and name of the conference where the citing papers appeared.”’
user_proxy.initiate_chat(graph_interrogator, message=msg)
Skipping the detail of the dialog, the final answer is

The failing here is that the graph does not have the year of the conference.
Here is another example:
msg = ”’find the topics of papers by Lawrence Snyder and find five other papers on the same topic. List the titles and proceedings each appeared in. ”’
user_proxy.initiate_chat(graph_interogator, message=msg)

Note: The acm topic for Snyder’s paper is “Operating Systems” and that is ACM topic D.4.
Final Thoughts
This demo is, of course, very limited. Our graph is very small. It only covers a small fraction of ACM’s topics and scope. One must then ask how well this scale to a very large KG. In this example we only have a dozen edge types. And for each edge type we needed a function that the AI can invoke. These edges correspond to the verbs in the language of the graph and a graph big enough to describe a complex organization or a field of study may require many more. Consider for example a large natural history museum. The nodes of the graph may be objects in the collection and the categorical groups in which they are organized, their location in the museum, the historical provenance of the pieces, the scientific importance of the piece and many more. The edge “verbs” could be extremely large and reflect the way these nodes relate to each other. The American Natural History Museum in New York has many on-line databases that describe its collections. One could build the KG by starting with these databases and knitting them together. This raises an interesting question. Can an AI solution create a KG from the databases alone? In principle, it is possible to extract the data from the databases and construct a text corpus that could be used to (re)train a BERT or GPT like transformer network. Alternatively, one could use a named entity recognition pipeline and relation extraction techniques to build the KG. One must then c